Chapter 9 Standard model of particle physics

This chapter introduces the building blocks that are required to understand the structure of the standard model of particle physics. It culminates in a detailed description of the relevant classical action functional that underlies this QFT. Further aspects of the standard model will be discussed in some of the student projects/presentations.

9.1 Brief overview

The standard model of particle physics is an impressive construct. It is a QFT that describes, very successfully, all observed fundamental particles in nature (electrons, neutrinos, quarks, …) and three of the four fundamental interactions (electromagnetic, weak and strong interaction). Unfortunately, the standard model does not include the gravitational interaction, which according to our current understanding can not be treated consistently within the framework of QFT. The issue is that the quantization of gravity leads to a non-renormalizable QFT (in the sense of Definition 8.2), hence our renormalization methods from Chapter 8 can not be applied to yield a predictive QFT for gravity. In contrast to that, the standard model of particle physics is a renormalizable QFT in \(d=4\) spacetime dimensions. During the past few decades there has been plenty of research towards constructing a theory of quantum gravity that resolves these issues, leading to viable candidates such as string theory and loop quantum gravity. However, a full understanding of quantum gravity is still elusive. It is important to stress that the problem of quantum gravity is more of a conceptual than practical nature: At the typical energy scales that are relevant for particle physics, say a few teraelectron volts \(\mathsf {TeV}\) as at the Large Hadron Collider (LHC), the gravitational interaction is extremely weak so that gravitational phenomena can usually be neglected. So a theory of quantum gravity is not necessarily needed for describing particle physics phenomena, which is the main reason why the standard model of particle physics (which excludes gravity) works so well in practice. However, in more extreme scenarios, such as in the early universe or in the vicinity of black holes, quantum gravity effects will become relevant so that an extension of the standard model to include gravity will eventually be required.

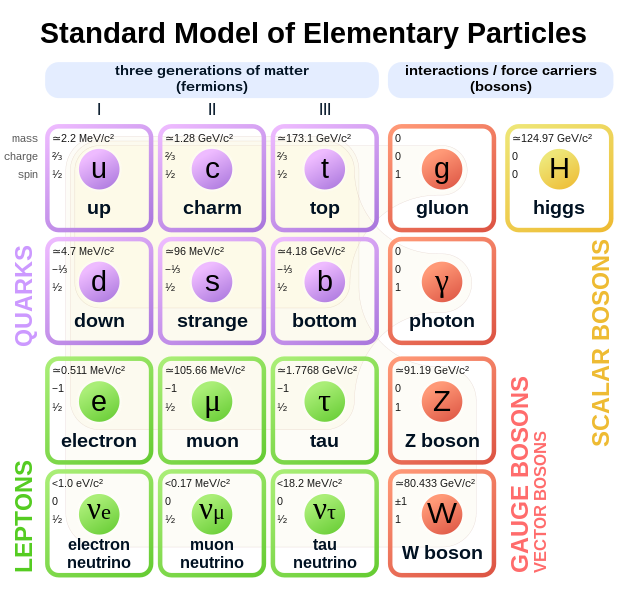
Explaining the standard model of particle physics is not so easy because, being a theory for all known fundamental particles and all their non-gravitational interactions, it is necessarily quite big. I think the best place to start is to look at the following schematic description (taken from the Wikipedia website) that nicely summarizes the particle content of the standard model:

Let us look more closely at this picture and extract some relevant information:

• • The fourth column lists the so-called gauge bosons of the standard model. We recognize an old friend, the photon \(\gamma \), which, as we have seen in Chapter 7, is the particle responsible for mediating the electromagnetic interaction. The other gauge bosons play a similar role: The \(W^+\), \(W^-\) and \(Z\) bosons mediate the weak interaction and the gluons \(g\) mediate the strong interaction. Hence, they are suitable generalizations (to be made precise in this chapter) of the electromagnetic potential/photon.

• • The first three columns list the matter fermions that are the building blocks for the matter observed in nature. Let us start by looking at the first column. We again recognize an old friend, the electron \(e\), which comes with an associated electron neutrino \(\nu _e\); you probably have heard before about neutrinos in the context of radioactive decays. The electron and its neutrino are among the so-called leptons, which are particles that do not participate in the strong interaction. The other two matter particles in the first column are the up quark \(u\) and the down quark \(d\). The word quark is used to describe particles that participate also in the strong interaction, in contrast to the leptons which do not. Quarks are the building blocks for composite (i.e. non-fundamental) particles called baryons and mesons, e.g. the proton is a bound state \(uud\) of two up and one down quark, and the neutron is a bound state \(udd\) of one up and two down quarks. Note that this means that we can build all atoms (i.e. the nuclei and their electron clouds) by using fundamental particles from the first column.

• • The particles in the second and third column are copies of the ones in the first column, which have the same properties but different (heavier) mass. For example, the muon \(\mu \) is a heavier cousin of the electron \(e\) and the tau \(\tau \) is an even heavier cousin. These three versions of the matter fermions (that are only distinguished by their masses) are often called the three generations.

• • Last but not least there is the fifth column, which contains the Higgs boson. This ingredient is somewhat special, because the Higgs is the only particle of spin \(0\) in the standard model, while all matter fermions have spin \(\frac {1}{2}\) and all gauge bosons have spin \(1\). The role of the Higgs is to give mass to the matter fermions, to some of the gauge bosons (namely the \(W^+\), \(W^-\) and \(Z\) bosons associated with the weak interaction) and also to itself through a mechanism that is called spontaneous symmetry breaking or the Higgs mechanism.

The aim of this chapter is to explain the mathematics behind these individual building blocks of the standard model as well as their interplay. We will start with the gauge bosons, i.e. the fourth column, which are the mediators of the electromagnetic, weak and strong interactions. They can be described by a non-trivial generalization of the electromagnetic potential and its gauge symmetries from Chapters 6 and 7, which are called (non-Abelian) Yang-Mills theories. The input for such theories is a choice of Lie group \(G\) that dictates the number of components of the gauge field, as well as their dynamics, and the structure of the gauge symmetries. For the Abelian group \(G=\mathsf {U}(1) = \{U\in \bbC : U^\ast \,U =1 \}\), Yang-Mills theory specializes to electromagnetism, hence it is indeed a generalization of the latter. The Lie group of the standard model of particle physics is the product \(G = \mathsf {U}(1)\times \mathsf {SU}(2)\times \mathsf {SU}(3)\) of the circle group \(\mathsf {U}(1)\) with the two-dimensional and the three-dimensional special unitary group. As we will understand at the end of this module, the factor \(\mathsf {U}(1)\times \mathsf {SU}(2)\) gives rise to the photon and the weak gauge bosons (these are \(\mathrm {dim}\big (\mathsf {U}(1)\times \mathsf {SU}(2)\big ) = 4\) many, namely \(\gamma \), \(W^+\), \(W^-\) and \(Z\)), while the factor \(\mathsf {SU}(3)\) gives rise to the \(\mathrm {dim}\,\mathsf {SU}(3) = 8\) many gluons \(g\).

Each generation of quarks and leptons in the first three columns is described by a certain family of Dirac fields in the sense of Chapter 5 that is suitably coupled to the gauge bosons via a generalization of the minimal gauge coupling construction from electromagnetism, see Section 7.1. We will later see that, in the context of Yang-Mills theory with Lie group \(G\), such coupling is determined by choosing a linear representation of \(G\) on a vector space \(V\). The punchline will be that the coupling between the gauge fields and a Dirac field \(\Psi : \bbR ^d\to \bbC ^N\otimes V\,,~x\mapsto \Psi (x)\) taking values in a representation \(V\) is governed by a suitable concept of covariant derivative. While the above captures the essence how a coupling between gauge fields and matter fermions can be established, the standard model comes with a small but physically important tweak: Since the standard model is defined in \(d=4\) spacetime dimensions, one can decompose a Dirac field \(\Psi = (\Psi _L,\Psi _R)\) into its left and right-handed chiral components, see the explanation around Eqn. (5.33). What happens in nature is that \(\Psi _L\) and \(\Psi _R\) participate differently in the interactions, which means that they take values in different representations of \(G\), say \(\Psi _L(x)\in \bbC ^2\otimes V_L\) and \(\Psi _R(x) \in \bbC ^2\otimes V_R\). So the standard model must be formulated using the finer concept of left and right-handed Weyl spinor fields, in contrast to Dirac fields that consist of both a left and a right-handed Weyl field. In short, people often say that the standard model is a chiral gauge theory as it treats left and right-handed chiralities differently.

The Higgs boson is described by a complex scalar field \(\Phi : \bbR ^d\to \bbC \otimes V_H\,,~x\mapsto \Phi (x)\) that couples to the gauge bosons through a suitable representation \(V_H\) of the Lie group \(G\). It also couples to the matter fermions through a so-called Yukawa interaction term in the action. These two kinds of couplings are crucial because, after spontaneous symmetry breaking, they will generate mass terms for the matter fermions and also for the \(W^+\), \(W^-\) and \(Z\) bosons.

You can now rightfully ask a lot of questions: How can someone come up with such a sophisticated and complicated model? Why is \(G = \mathsf {U}(1)\times \mathsf {SU}(2)\times \mathsf {SU}(3)\) the correct choice of Lie group? How do I choose the correct representations \(V\) of \(G\)? Why are there three generations of matter, and not only \(1\) or as many as \(42\)? These are indeed good questions that people have thought about, but I think that nobody has a good answer. Our current mathematical description of the standard model requires us to make certain choices along the way, such as the Lie group \(G\), its representations, the number of generations and some numerical parameters in the action functional, all of which require experimental input. In fact, the development of the standard model of particle physics took various decades, and it was due to a constant back-and-forth between experiment and theory that such a successful model for fundamental physics could be developed.